KNN - 近朱者赤 近墨者黑
初接觸Machine Learning的朋友們,對KNN這個算法應該也不陌生了,原理既容易理解,應用也十分廣泛,只要有足夠的鄰居(訓練數據),也可以用作分類或迴歸(Regression)的方面工作。舉一個活活的例子,中學時代(當時還沒有Online social platform,感嘆時代的變遷)總會遇上一個暗戀對象,但對他/她的背景認識還未夠深,便會傾向留意和觀察他/她身邊的朋友是那種人,從而判斷他/她是一個怎麼樣的人。正所謂近朱者赤,近墨者黑,而是近硃砂的會被判定為染成紅色,靠近墨的則是黑色,也同時寓意Testing Data的預測結果因環境(Training Data)所影響的。
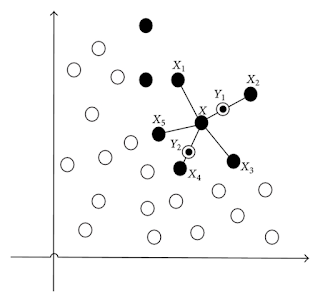
KNN屬於機器學習中的Supervised learning其中一種算法,從訓練數據的Label進行學習,建構好的模型要,首先要知道KNN全名為K-nearest neighbors,即利用k個最近似的鄰居,最後"以多數服從少數"的方式判斷該人/事是屬於那種類別。為了讓讀者明白整個算法的原理,有9個數據點,其中8個來自Training Data,分別有4個藍色的,4個紅色的;至於中間有一紅點,它是來自Testing Data的,最一開始我們是不知道它是紅還是藍的,假設我們用3位鄰居(k = 3)便決定是什麽,會發現其中兩個是紅的,另外一個是藍的,根據"多數服從少數",這個被判斷為紅色,最後也因此我把它變成紅色了。
把以上的原理拓展到更多的數據量,更多的Features,更多的類別(Class),便能應用在各式各樣的Business / Research Problem。不過要深入理解這個Algorithm的設計,了解到這個程度是還不足夠的,我們還需要明白以下的學問包括:
要判斷那些是鄰居的話,首先要量化相似度,而Eulidean Distance是比較常用的方法來量度相似度:
$Distance = \sqrt{\sum_{i=1}^{k} (x_{i}-x_{self})^2}$
(注:Eulidean Distance只是其中一個量化距離的方法,其他的例如Manhattan Distance,在High Dimension高維度甚至會發揮得更好,所以當在選擇什麼方法的時候,應該要先了解手上的數據。)
鄰居顧名思義是最接近自己的人,所以距離愈短的則是鄰居,k個距離的便順利成章成為鄰居。
要多少個鄰居(k)才夠呢?
至於多少個鄰居才夠,這涉及到Fitting的議題,太少的鄰居會導致過度相信鄰居的特性,不夠代表性,當換成另一組人(即訓練數據),模型預測便失準了,這個問題稱為Overfitting;相反,過多的鄰居則變成隨波逐流,跟大隊走,也就是Underfitting。另外,雙數的鄰居令少數服從多數的機制失效,要用較複雜的機制來決定。因此,優化k這個參數是需要一定的技巧的。
KNN除了能夠做分類之餘,也可以做Regression,原理基本上和剛才提到的一樣,只是預測的目標由類別變成了數字而已。
Programming方面,我就不多解釋了,現在的package實在太方便了,而documentation也非常完整。R用class的package,knn這個function會為你效勞(注:knn function的第三個argument為y label,記得用factor function把y由vector轉換成factor才放進function裡。而Python的話用上Scikit-Learn的NearestNeighbors就可以了。
KNN屬於機器學習中的Supervised learning其中一種算法,從訓練數據的Label進行學習,建構好的模型要,首先要知道KNN全名為K-nearest neighbors,即利用k個最近似的鄰居,最後"以多數服從少數"的方式判斷該人/事是屬於那種類別。為了讓讀者明白整個算法的原理,有9個數據點,其中8個來自Training Data,分別有4個藍色的,4個紅色的;至於中間有一紅點,它是來自Testing Data的,最一開始我們是不知道它是紅還是藍的,假設我們用3位鄰居(k = 3)便決定是什麽,會發現其中兩個是紅的,另外一個是藍的,根據"多數服從少數",這個被判斷為紅色,最後也因此我把它變成紅色了。
把以上的原理拓展到更多的數據量,更多的Features,更多的類別(Class),便能應用在各式各樣的Business / Research Problem。不過要深入理解這個Algorithm的設計,了解到這個程度是還不足夠的,我們還需要明白以下的學問包括:
誰是鄰居們?誰是鄰居們?
要多少個鄰居(k)才夠呢?
要判斷那些是鄰居的話,首先要量化相似度,而Eulidean Distance是比較常用的方法來量度相似度:
$Distance = \sqrt{\sum_{i=1}^{k} (x_{i}-x_{self})^2}$
(注:Eulidean Distance只是其中一個量化距離的方法,其他的例如Manhattan Distance,在High Dimension高維度甚至會發揮得更好,所以當在選擇什麼方法的時候,應該要先了解手上的數據。)
鄰居顧名思義是最接近自己的人,所以距離愈短的則是鄰居,k個距離的便順利成章成為鄰居。
要多少個鄰居(k)才夠呢?
至於多少個鄰居才夠,這涉及到Fitting的議題,太少的鄰居會導致過度相信鄰居的特性,不夠代表性,當換成另一組人(即訓練數據),模型預測便失準了,這個問題稱為Overfitting;相反,過多的鄰居則變成隨波逐流,跟大隊走,也就是Underfitting。另外,雙數的鄰居令少數服從多數的機制失效,要用較複雜的機制來決定。因此,優化k這個參數是需要一定的技巧的。
KNN除了能夠做分類之餘,也可以做Regression,原理基本上和剛才提到的一樣,只是預測的目標由類別變成了數字而已。
Programming方面,我就不多解釋了,現在的package實在太方便了,而documentation也非常完整。R用class的package,knn這個function會為你效勞(注:knn function的第三個argument為y label,記得用factor function把y由vector轉換成factor才放進function裡。而Python的話用上Scikit-Learn的NearestNeighbors就可以了。



Comments
Post a Comment